TREE (Pohon)

Dalam ilmu komputer, tree adalah sebuah struktur data yang secara bentuk menyerupai sebuah pohon, yang terdiri dari serangkaian node (simpul) yang saling berhubungan. Nodenode tersebut dihubungkan oleh sebuah vektor.

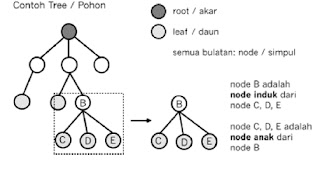
Setiap node dapat memiliki 0 atau lebih node anak (child). Sebuah node yang memiliki node anak disebut node induk (parent). Sebuah node anak hanya memiliki satu node induk. Sesuai konvensi ilmu komputer, tree bertumbuh ke bawah, tidak seperti pohon di dunia nyata yang tumbuh ke atas.

Dengan demikian node anak akan digambarkan berada di bawah node induknya. Node yang berada di pangkal tree disebut node root (akar), sedangkan node yang berada paling ujung pada piramida tree disebut node leaf (daun).

Binary Tree (Pohon Biner)

Dalam mata kuliah struktur data, secara khusus akan dipelajari mengenai pohon biner. Pohon biner adalah sebuah tree yang pada masing-masing simpulnya hanya dapat memiliki maksimum 2 (dua) simpul anak. Tidak boleh lebih. Pada pohon biner, umumnya kedua node anak disebut dengan posisinya, yaitu kiri dan kanan.

Beberapa istilah pada pohon biner:

·         Size (ukuran): jumlah total node yang terdapat pada pohon biner tersebut.

·         Depth (kedalaman): panjang jalur yang menghubungkan sebuah node sampai ke node anaknya yang paling ujung (leaf). Depth biasa juga disebut height.

·         Full Binary Tree (Pohon Biner Penuh) adalah pohon biner yang setiap nodenya pasti memiliki 0 atau 2 node anak.

·         Perfect Binary Tree (Pohon Biner Sempurna) adalah pohon biner yang semua node leafnya berada pada kedalaman yang sama dari node root. Juga disebut sebagai Complete Binary Tree (Pohon Biner Lengkap)

·         Almost Complete Binary Tree (Pohon Biner Hampir Lengkap) adalah pohon biner yang setiap nodenya dapat memiliki 0 node anak, atau memiliki kiri, atau jika memiliki kanan harus memiliki kiri. Tidak boleh memiliki kanan saja.

Implementasi

Implementasi dalam pemrograman, dalam pokok bahasan ini akan dibicarakan untuk pohon biner saja. Asumsi awal adalah data yang hendak dimasukkan ke dalam node, bertipe data integer.

1. Deklarasi Tree

Karena tree tersusun oleh node-node, maka yang perlu kita deklarasikan adalah komponen node itu sendiri. Dalam contoh dibawah, akan kita namai Node. Sebelumnya perlu kita lihat bahwa untuk mewujudkan implementasi node ke dalam bahasa pemrograman, diperlukan sebuah struktur yang memiliki susunan berikut ini:

Variabel data digunakan untuk menyimpan nilai angka node tersebut, sedangkan kiri dan kanan, bertipe pointer, masing-masing mewakili vektor yang akan menunjuk ke node anak kiri dan kanan.

2. Inisialisasi Tree

Untuk pertama kali, saat kita akan membuat sebuah pohon biner, asumsi awal adalah pohon itu belum bertumbuh, belum memiliki node sama sekali, sehingga masih kosong. Oleh karena itu perlu kita tambahkan kode berikut pada baris awal prosedur Main

3. Menambahkan Node Pada Tree

Karena pohon yang kita buat merupakan sebuah pohon biner, maka untuk menambahkan sebuah node, secara otomatis penambahan tersebut mengikuti aturan penambahan node pada pohon biner:

1.    Jika pohon kosong, maka node baru ditempatkan sebagai akar pohon.

2.    Jika pohon tidak kosong, maka dimulai dari node akar, dilakukan proses pengecekan berikut:

a.    Jika nilai node baru lebih kecil dari nilai node yang sedang dicek, maka lihat ke kiri node tersebut. Jika kiri node tersebut kosong (belum memiliki kiri), maka node baru menjadi kiri node yang sedang dicek. Seandainya kiri node sudah terisi, lakukan kembali pengecekan a dan b terhadap node kiri tersebut. Pengecekan ini dilakukan seterusnya hingga node baru dapat ditempatkan.

b.    Jika nilai node baru lebih besar dari nilai node yang sedang dicek, maka lihat ke kanan node tersebut. Jika kanan node tersebut kosong (belum memiliki kanan), maka node baru menjadi kanan node yang sedang dicek. Seandainya kanan node sudah terisi, lakukan kembali pengecekan a dan b terhadap node kanan tersebut. Pengecekan ini dilakukan seterusnya hingga node baru dapat ditempatkan.

4. Membaca dan Menampilkan Node Pada Tree

Untuk membaca dan menampilkan seluruh node yang terdapat pada pohon biner, terdapat 3 macam cara, atau yang biasa disebut kunjungan (visit). Semua kunjungan diawali dengan mengunjungi akar pohon. Karena proses kunjungan ini memerlukan perulangan proses yang sama namun untuk depth yang berbeda, maka ketiganya diimplementasikan dengan prosedur rekursif.

Kunjungan Pre-Order.

Kunjungan pre-order dilakukan mulai dari akar pohon, dengan urutan:

1.    Cetak isi (data) node yang sedang dikunjungi

2.    Kunjungi kiri node tersebut,

a.    Jika kiri bukan kosong (NULL) mulai lagi dari langkah pertama, terapkan untuk kiri tersebut.

b.    Jika kiri kosong (NULL), lanjut ke langkah ketiga.

3.    Kunjungi kanan node tersebut,

a.    Jika kanan bukan kosong (NULL) mulai lagi dari langkah pertama, terapkan untuk kanan tersebut.

b.    Jika kanan kosong (NULL), proses untuk node ini selesai, tuntaskan proses yang sama untuk node yang dikunjungi sebelumnya.

Kunjungan In-Order.

1.    Kunjungi kiri node tersebut,

a.    Jika kiri bukan kosong (NULL) mulai lagi dari langkah pertama, terapkan untuk kiri tersebut.

b.    Jika kiri kosong (NULL), lanjut ke langkah kedua.

2.    Cetak isi (data) node yang sedang dikunjungi

3.    Kunjungi kanan node tersebut,

a.    Jika kanan bukan kosong (NULL) mulai lagi dari langkah pertama, terapkan untuk kanan tersebut.

b.    Jika kanan kosong (NULL), proses untuk node ini selesai, tuntaskan proses yang sama untuk node yang dikunjungi sebelumnya.

Kunjungan Post-Order.

1.    Kunjungi kiri node tersebut,

a.    Jika kiri bukan kosong (NULL) mulai lagi dari langkah pertama, terapkan untuk kiri tersebut.

b.    Jika kiri kosong (NULL), lanjut ke langkah kedua.

2.    Kunjungi kanan node tersebut,

a.    Jika kanan bukan kosong (NULL) mulai lagi dari langkah pertama, terapkan untuk kanan tersebut.

b.    Jika kanan kosong (NULL), lanjut ke langkah ketiga.

3.    Cetak isi (data) node yang sedang dikunjungi. Proses untuk node ini selesai, tuntaskan proses yang sama untuk node yang dikunjungi sebelumnya.

Variabel **root pada setiap fungsi diatas menunjukkan node mana yang sedang dikunjungi saat ini, untuk itu saat pemanggilan, variabel **root kita beri nilai pointer yang menunjuk ke node akar, yaitu pohon.

Double Link List

Pada minggu lalu kita mempelajari tentang link list dimana pada link list ini hanya memiliki 1 buah pointer saja. Hal ini menyebabkan bahwa link list hanya bisa dibaca satu arah saja. Yaitu dari kiri ke kanan. Hal ini kurang cepat jika kita ingin mencari data pada link list.

Untuk mengatasi penggunaan link list maka kita menggunakan double link list yaitu link list yang mempunyai 2 buah pointer. Dimana 1 pointer menunjuk ke alamat berikutnya dan 1-nya lagi menunjukkan ke alamat sebelumnya.

Double link list adalah link list yang memiliki dua buah pointer yang menunjuk ke simpul sebelumnya (Prev) dan yang menunjuk ke simpul sesudahnya (Next).

Double Link list dapat digambarkan seperti berikut ini :

Ada beberapa hal yang harus diketahui mengenai Double link list, diantaranya adalah :

1.    Double Link list selalu memiliki pointer petunjuk yang selalu menunjuk pada awal dari list yang disebut Head.

2.    Double Link list juga selalu memiliki pointer petunjuk menunjuk pada akhir dari list yang disebut Tail.

3.    Setiap simpul yang terbentuk selalu memiliki nilai NIL, kecuali jika simpul tersebut sudah ditunjuk oleh simpul yang lainnya (Double Link list belum terhubung).

4.    Posisi simpul terakhir pada Doube link list selalu bernilai NIL karena ia tidak menunjuk pada simpul yang lainnya, kecuali bentuk circular.

5.    Operasi yang dapat dilakukan pada DoubleLink list diantaranya adalah :

a.    Inisialisasi.

b.    Menambah Simpul (di Depan, Belakang dan Tengah).

c.    Menghapus Simpul (di Depan, Belakang dan Tengah).

d.    Membaca isi link list (Membaca maju dan mundur).

Circular Double Link List

Jenis link list ini merupakan jenis double link list yang memiliki simpul kepala dan tidak mempunyai tail (Head = Tail). Fungsi simpul kepala dapat digunakan untuk menyimpan informasi tambahan pada list. Berikut ini merupakan ilustrasi dari circular header double link list.

Beberapa Operasai pada circular double link list :

Inisialisasi

Proses ini dilakukan untuk mendefinisikan Circular double link list untuk pertama kalinya atau dengan kata lain ingin membuat Head. Pada proses ini kita menginginkan agar pointer kiri (Prev) dan kanan (Next) dari simpul kepala tidak bernilai NIL, sehingga simpul kepala pada saat inisialisasi bisa kita gambarkan sebagai berikut :

Menambah Simpul

Menambah simpul pada double link list ada tiga macam yaitu menambah di depan, belakang dan tengah, tapi hanya penambahan yang umum dipakai saja oleh double link list yang akan dibahas yaitu penambahan simpul di belakang. Penambahan di belakang maksudnya menambahkan simpul-simpul baru pada posisi Tail

Menghapus Simpul

Operasi menghapus simpul juga ada tiga macam yaitu menghapus simpul di depan, belakang dan tengah. Tapi dengan menggunakan double link list proses pencarian simpul yang akan dihapus menjadi semakin cepat. Untuk menghapus sebuah simpul diperlukan satu buah tambahan variabel pointer yaitu variabel bantu yang berguna untuk menunjukkan simpul manakah yang akan dihapus

Membaca Isi dari simpul

Dengan menggunakan double link list proses pembacaan simpul dapat dilakukan dua arah tanpa harus dilakukan prosedur membalik simpul. Kita hanya menggunakan satu prosedur bantu yang pointer next-nya kita gunakan jika kita ingin membaca mundur atau pointer prev-nya jika kita ingin melakukan pembacaan secara maju.